[音声の音響分析 レイ・D・ケント/チャールズ・リード著、荒井隆行/菅原 勉 監訳 28頁]
2.1.4 摂動理論
摂動理論(Perturbation Theory)を用いると、共鳴管の摂動(局所的な狭め)によって生じるフォルマント周波数の変化を予測することができるようになる。これは強力な理論であり、母音のフォルマント周波数を説明できるという理由から、音声生成の音響学にとって特に重要である。
この理論がどのように母音生成に適用されるのかを見るために、図2-12に示されるように声道を単一音響管で表現することにする。この単一音響管モデルは今日ではよく知られているはずであり、このような管は各共鳴周波数において定在波の体積速度分布(あるいは、それとは逆の関係にある圧力分布)を有する。基本的に、菅が共鳴している際に於ける体積速度の変化は、個々の粒子が管の中のさまざまな位置でどのように振動しているかということを反映している。ある場所では粒子の振動は最小となり(このとき圧力はもっとも高い)、また別のある場所では粒子の振動は最大となる(このとき圧力はもっとも低い)。粒子の振動振幅が最小になるところでは体積速度が最小であり、その箇所は“節“(node)と呼ばれる。粒子の振動振幅が最大になるところでは体積速度が最大であり、その箇所は“腹”(antinode)と呼ばれる。体積速度(あるいはそれと逆の関係にある圧力)が管に沿って定常的な分布を持つということは、管共鳴の特徴である。管は無限の数の共鳴周波数を持ち、体積速度分布(あるいは圧力分布)は個々の共鳴に対して記述できるわけだが、ここでは母音の第1から第3フォルマントに対応させ管の3つの共鳴に議論を限定する。ついでに言えば、これらの定在波を実験的に確かめることも可能である。ノーベル賞受賞者であるGeorg von Bekesy (1960) は、話者が母音を生成している最中に、小さなマイクロフォンをその人の声道内でゆっくりと移動させることによって、声道内での圧力変化を実際に示した。マイクロフォンの出力からは、定在波の圧力変化に対応する最大値と最小値が観察された。
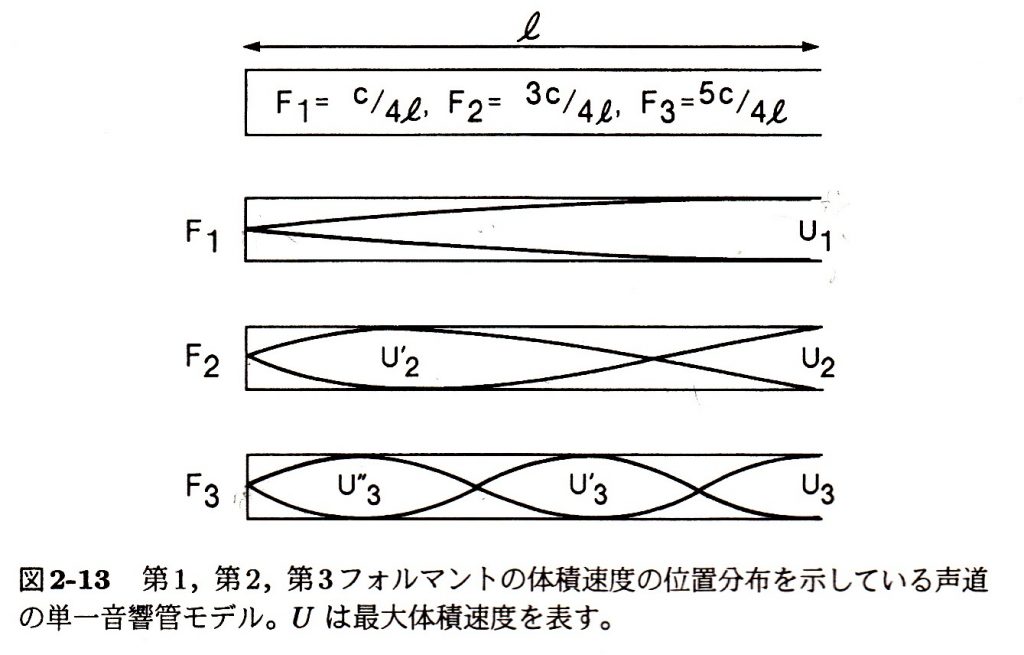
図2-13に示されているように、第1共鳴の定在波分布は開いた端(声道に於ける唇側の端)に最大体積速度(すなわち腹)を持ち、閉じた端(声道に終える声門側の端)に最少体積速度(すなわち節)を持つ。第2共鳴は2つの最大体積速度(腹)と2つの最少体積速度(節)を、第3共鳴は3つの最大体積速度と3つの最少体積速度を持つ。言い換えれば、声道の任意の共鳴Fnはn個の腹と節を持つ(ただしnは整数)。
図2-12の共鳴管が柔軟な素材からできていて、押さえればどこでも狭めを作ることができると仮定しよう。そのようにしてつくられた狭めは摂動の原因となり、その摂動がフォルマントFnに及ぼす効果は、その狭めが節に近いか腹に近いかに依存している。一般的には次のような関係がある。
- 局所的な狭窄が最大体積速度(腹)の近くにある場合、フォルマント周波数は低くなる。
- 局所的な狭窄が最小体積速度(節)の近くにある場合、フォルマント周波数は高くなる。
さて、図2-12を人間の声道に近似させるため、図2-14のように描き直してみよう。図2-14の記号NとAはそれぞれ節と腹を表す。NとAの下に添えられている数字は、フォルマントを表す。つまり、たとえはA1とあればこれは第1フォルマント(F1)の腹(すなわち最大体積速度)を表すことになる。声道に作られる狭めは、上に述べた2つの関係に従って、中声母音(neutral vowel)/ɘ/のフォルマント周波数を変化させることになる(中声母音は声道に狭めを作らずに生成される)。腹Ⓐでの狭めはF1とF2の両方を低くする(実際は、唇が狭められるとすべてのフォーマントが狭くなる)。節Ⓑでの狭めはF2を高く、腹Ⓒでの狭めはF2を低くする。これらの関係が個々の母音にどのように当てはまるのか考えてみよう。母音/i/(“he”)は硬口蓋(節Ⓑの近く)に狭めを持ち、したがって低いF2を持つ。母音/a/(”ha”)は咽頭(腹Ⓒの近く)に狭めを持ち、したがって低いF2を持つ。母音/u/は唇(腹Ⓐ)に狭めを持ち、したがって低いF1とF2を持つ。このように、摂動理論は声道内の狭めがフォルマント周波数にどのような影響を及ぼすかについての予測を可能にするのである。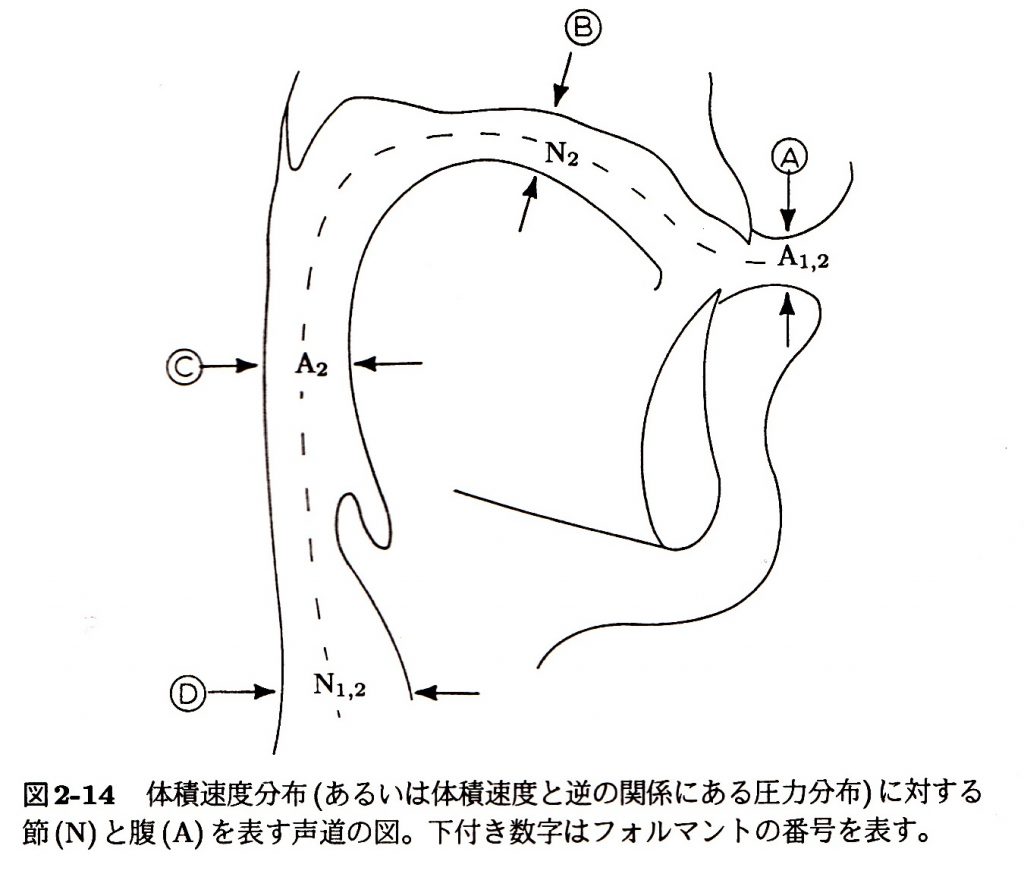
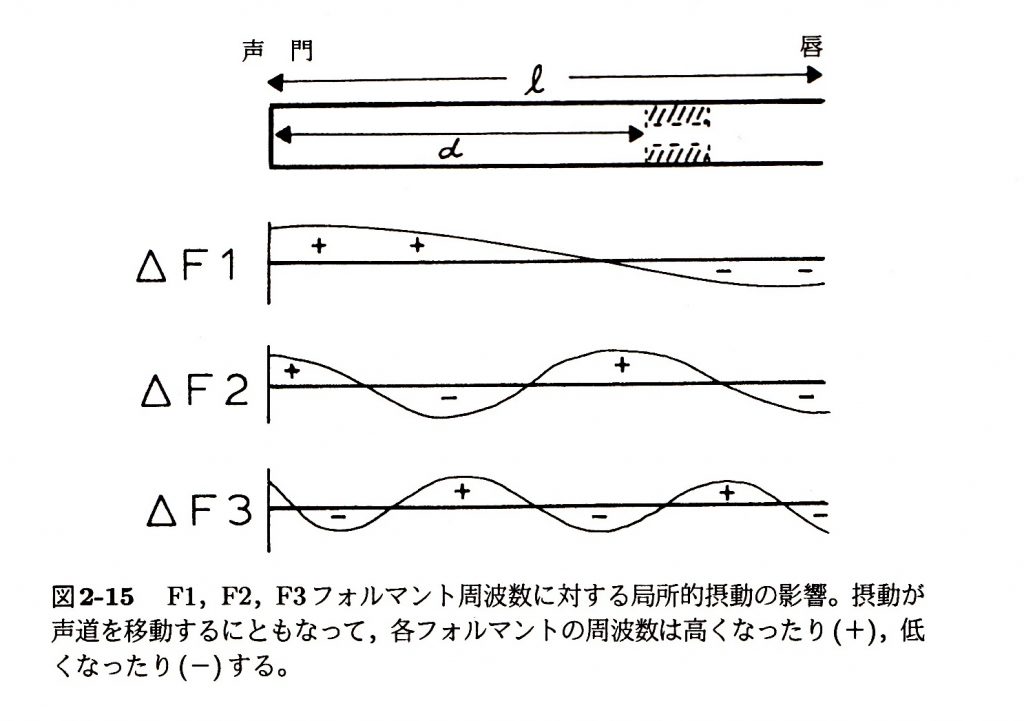
摂動理論による予測を示す最後の例として、図2-15において単一音響管内の狭めがF1,F2,F3の周波数にどのような影響を及ぼすかを説明する。プラス記号(+)はその地点での狭めがフォルマント周波数を高くすることを表し、マイナス記号(-)はその地点での狭めがフォルマント周波数を低くすることを表す。特に次のようなこうかについて注目してほしい。
- 唇での狭めは3つのフォルマントすべてを低くする。
- 喉頭近くでの狭めは3つのフォルマントすべてを高くする。
- F2に対する曲線においてマイナス記号で示されている領域は母音/ɑ/生成時の舌による狭めの位置に対応する。
- F3に対する曲線においてマイナス記号で示される領域は、唇・硬口蓋・咽頭での狭めに対応する(これはアメリカ英語の/r/がいくつかの異なった方法で生成されることを理解する手助けとなる。この/r/は通常、舌尖を歯茎後部に向かって反り返らすことで生成されるが、時に、硬口蓋に狭めを設けたり、あるいは時に、咽頭に狭めを設けることで生成される。というのも、これら3つの領域での狭めはすべてF3の低下と結びつくからである)。
上の1.についてさらにコメントすると、以前、唇を丸めると声道の長さが長くなるので、円唇化はすべてのフォルマントの周波数を低くするということを述べた。しかし、話者のなかには唇を突き出すことなく狭めるだけでフォルマントの周波数を低くしている者もいるのである。これはどうして可能なのだろうか。図2-13、2-14、2-15を調べると、その答えが得られる。唇ではどのフォルマントに対しても体積速度が最大である。したがって、この位置での狭めはあらゆるフォルマントの周波数を低くする。実際、話者がすべてのフォルマントの周波数を低くするには3つの一般的方法がある。すなわち、(1)唇を突き出して声道を長くする、(2)唇に狭めをつくる、(3)喉頭を下げる(これは声道を長くするもう1つの方法)、である。