Preclinical Speech Science 2008
by Thomas J. Hixon, Gary Weismer, Jeannette D. Hoit
6 Acoustics p. 317
PRESSURE WAVES
圧力波
このセクションは、圧力波の性質を考える。それは、そのような波を制御する力、どのように空気の密度が局所的に変わるのか、どのように圧力波がスペースを通って広がるのか、そして、そのような波がどのように測定され表示することができるかを議論する。
振動している空気分子の動作は、単純な力によって決定される
音は空間と時間における圧力波 ― 音波(sound wave) ― の伝播と定義できる。この定義の解明は、圧力波という語によって精確に意味されることの厳密な定義を必要とする。
音は、常になんらかの媒質(medium)を通して伝達される。音波を伝えるであろうさまざまな媒体(例えば、水、鋼、空気)はすべて、多かれ少なかれ圧縮できる分子から成る。言い換えると、これらの媒体の分子は ― 力の影響を受けて ― それらの静止位置(「静止位置」とは媒質に力が加えられていない位置)から変位されて隣接する分子へ接近するだろう。静止状態の分子の分布と比べて、結果として生じる分子の『一か所に集まる(bunching up)』ことは、媒質が圧縮可能であることを示している。
すべての音響伝導媒体の分子は、さらに弾性(elasticity)と質量(mass)の特徴を共有する。弾力性がある物は変位 (displacement)に対抗して、それらが静止位置からより遠くに動かされるほど大きな規模で対抗する。これに対して一般によく引用される例は、ゴムバンドである。ゴムバンドが完全に縮んでいるとき、それは静止位置にある。ゴムバンドは引っ張られるほど、固くなり次第に引っぱるのが難しくなる。大きい物体は、加速と減速に対抗する(つまり、それらは慣性(inertia)を持つ)、そして、物体が大きくなるほど大きな規模で対抗する(「動いている物体は、そのまま動き続けようとする傾向がある」)。運動時における質量の影響は、ブレーキがかけてもすぐに止まらないスピード違反の自動車の例で簡単に理解することができる。変位(弾力)と加速/減速(質量)への対抗は、実際にエネルギーの蓄積になる。この保存されたエネルギーは、外からの力が加わらない場合オブジェクト・イベントの運動と言うことができる。この論題は、後で更に詳しく論じられる。
スピーチに関して音を伝える媒質は、少なくともほとんどの場合空気である。ギリシア文字ロー(ρ)の符号であらわされ、空気の密度 (density)と呼ばれる1立方インチ(16.39立方センチ)の空気の分子の数はおよそ4 x 10²³である。水の分子の密度は空気よりおよそ4倍多く、鋼では空気より11倍多い。
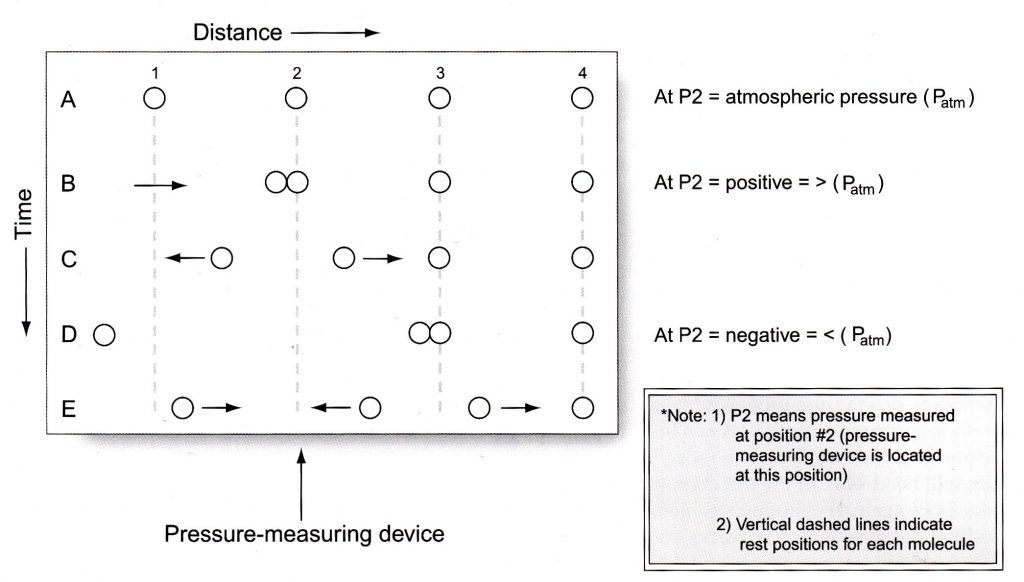
図6-1.
静止位置周辺の空気分子の振動の図解モデル。
4つの分子の静止位置は、1、2、3、4で示される。
時間は、A、B、C、D、Eの横列によって示される。
圧力測定装置は、分子2の静止位置にある。
詳細はテキストを見なさい。
列A ― P 2 =大気圧(Patm)
列B ― P 2 =プラスの=>(Patm)
列D ― P 2 =マイナス=<(Patm)
注:1)P 2は、位置#2(圧力測定装置はこの位置にある)で測られる圧力を意味する
2)垂直点線は、各々の分子のために静止位置を示す
媒質としての空気について、概略図が上記の概念を例示して圧力波の性質をはっきりさせるのに用いられることができる。図6-1で示すように、空気分子(1、2、3、4の番号が付いた)の等間隔の4つの柱を想像しなさい。A、B、C、D、Eと記された5本の横列は、連続した適時の瞬間の分子の状態を示す。A列(以下、時間A)は、外部の力が加わらない静止している分子を示す。この静止位置は、分子の4本の柱の全体を通じて下に延びる点線によって、すべての時間を通じて示される。時間Aの全域での分子の均一な間隔に注意しなさい。静止時の分子は実際のところ動いていない(この静止運動はブラウン運動(Brownian motion)と呼ばれる)、しかし、分子の間の平均的間隔は、図6-1、時間Aで示すようにだいたい等しい。時間Aの分子がそれらの静止位置から変位されてなく、それゆえ加速されていないので、それらは弾性または慣性エネルギー(ブラウン運動(Brownian motion)のための小さな蓄積されたエネルギー以外の)を蓄積しない。時間Bで柱1の分子は、静止位置から右側(右向きの矢印で示される)に離れて位置2の分子の方向に動かす力 (force)を受ける。当面の目的のために、力 (force)とはいかなる押しまたは引きでも物体に作用するものとして考えることができる。移動する分子はその静止位置からより遠くなるほど、増加する反跳力 (recoil force)を生む、それによって変位の増加に対抗する、 そしてそれは静止位置に、または、現行の運動方向とは逆の方向に押し戻される。別の角度から言うと、右へ押す最初の力は、空気の分子を移動させ、その右への変位は、その静止位置へ戻ってはね返えろうとする分子の傾向によってますます抵抗される。現行の運動は、最初の押しの力がまだ反跳力を上回るので静止位置から離れ続ける。反跳力は、分子の変位から生じる蓄積されたエネルギーであり、それらの静止位置から変位させられたすべての弾力性を持つ物体の特質である。
位置2、時間Bで、いくつかの興味深いことが起こる。第1には、分子1と2の間隔は、今やそれらの静止位置(時間A)での間隔と比べて最小である。位置2(時間B)で、分子は集められ分子1は分子2にぶつかる 。それはちょうど、最初にその押しがこのプロセスを進行させるために分子1にぶつかったのとちょうど同じである。第2には、プロセスを開始するために、最初に押された分子は、先に述べたように、その静止位置から比較的遠くに変位させられて静止位置に戻るために強い反跳力を生じている。ある時点で、反跳力は最初の力に等しが、その後には上回り、それが分子の右への運動を止めて左へ動く原因となる。位置1からの最初の分子が時間Bで 、ただ分子を位置2にぶつけるだけでなく、その方向を逆にしようとしていると考えなさい。方向の逆転は、最初の押しによる分子に向かう力にまさる反跳力によってなされる。
時間Cで、位置1からの分子は、静止位置の方(左向きの矢)へ戻る。位置2からの分子は、位置1の分子によってぶつけられ、今その静止位置から離れ位置3の分子の方向(右向きの矢)に移動する。時間Dで、位置2からの分子は、位置3で分子にぶつかっていてさらにその方向を今や逆にしようともしている 。ちょうど時間B、位置2での上述の状況のように。しかし、位置1からの分子はその静止位置を通り抜けて、左に遠く変位させられる-時間Dで位置1と2の分子による広い分離に注意しなさい。明らかに、弾性収縮力は時間E、位置2で、分子を静止位置の方へ戻そうとするが、なぜその運動は静止位置で止まらないのか? 答えは、慣性力が分子を静止位置で「直ちに止まらせ」ず、静止位置を通り越して左端に分子を押しやるということである。分子(それには質量があり、加速と減速に対抗する)は、すぐに静止位置で止まるために減速せず、むしろ空間のそのポイントを通り越して運動を続ける。反跳力が分子を静止位置から追いやる力(主に慣性)に再び勝つまで、運動は左方向に続くだろう。この時、その運動はもう一度逆にされ、分子は静止位置の方向に戻る。再度、運動は静止位置で慣性力のため止まらない、そして、分子は静止位置の前後を行きつ戻りつして動き続ける。
位置1での力の最初の適用の後、その前後の動きは、反跳力と慣性力の形で分子自体に蓄積されたエネルギーによって維持される。分子が摩擦のない (frictionless)媒質の中で振動しているならば 、熱を生み出すためのエネルギーがないところでは、前後運動は際限なく続くだろう。実際には、空気分子のどうしの摩擦や他の表面との摩擦のための熱損失は、外部の力が空気分子に絶えず加わり続けていなければ、いつかは前後運動を消滅させるだろう。しかしながら、反跳力と慣性力の原理がさらに消滅運動に加わる。そして、摩擦力は、外部の力がない場合、反跳力と慣性力と張り合うだけで外部の力(例えばもう一つの押し)がない場合、最終的に後の2つが優位を占め運動を終える。
振動している空気分子の動作は、空気の局部密度を変える
空気分子の運動と、その運動をコントロールする力は説明された。これらの考察はどのように圧力波の理解に導くことがができるか? 気圧の測定装置が図6-1の位置2に置かれると仮定しなさい。圧力 (pressure)は単位面積(P =F/A)に働く力として定義されることができ、空気の密度 (density)と比例する。空気分子が高密度に詰め込まれるとき、それらはたびたび互いと衝突して、多くの力と多くの圧力を発生させる。反対に 、空気分子が一か所に高密度に詰め込まれなければ、衝突はより少なく、圧力は比較的低い。図6-1の時間Aで、空気分子に加えられる外部の力がなく、空気の密度は静止時の空気と結びつく(上記の4×10の23乗の数字を思い出す)。時間A、位置2(または、静止時の空気の密度はどんな空間的位置でも同じなので、時間Aの他のどの位置でも)で測定された圧力は大気圧 (atmospheric pressure)と呼ばれる。大気圧の実際の値は今の議論(2)にとって重要でない、しかし、この圧力の基準関数 (reference function)は重要である。以下の説明において、大気圧(これ以降Patmで表わす )は、ゼロ(0)圧と考えられる。時間Bで、概略図は2つの分子が接近することを示し、時間Aと比較して空気分子の比較的高い密度の集合が明らかになる。時間B、位置2での圧力測定装置は、時間Aより高い圧力を測定するだろう、なぜならば、分子の密度の高さはより頻繁な衝突とより高い力を伴うから。圧力が基準圧力Patmを越えるならば、それは陽圧 (positive pressure)と呼ばれる。分子がよりしっかりと引き寄せられるほど、圧力はよりプラスとなる。
(注2)海面の大気圧は、1平方インチにつき14.7ポンド(約453.6グラム)または1013ミリバール(圧力の替わりの単位)である。
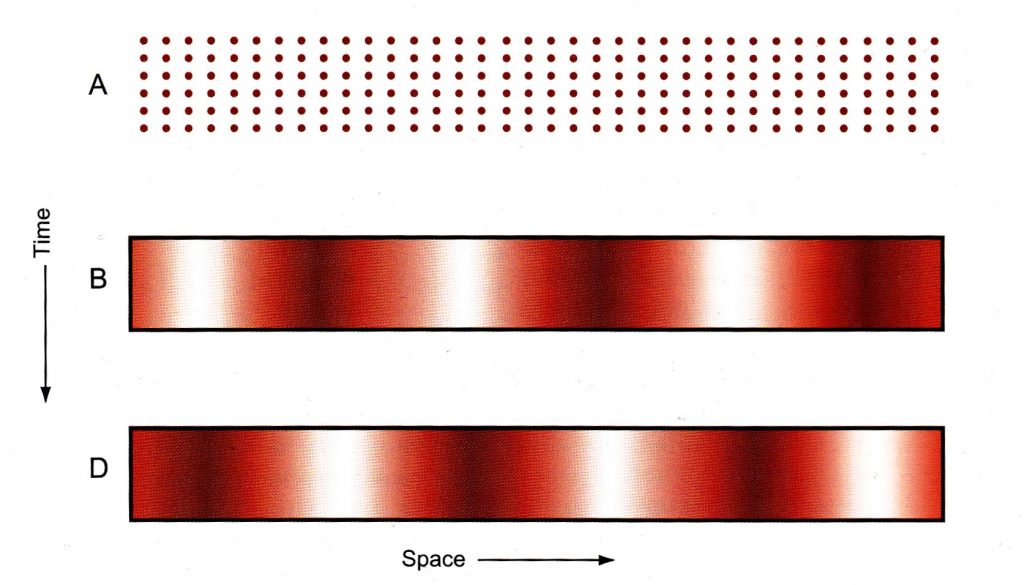
図6-2.
空間と時間に分配された圧力波の概略図面。
A、BとDは、図6-1の中で表される別々の時間と一致する。
空間の特定の点で、圧力は時間とともに変わる。
時間D、位置2では、1および2番目の分子は広いスペースで引き離される。これは、空気密度がPatmより少ないケースを意味する。圧力測定装置はPatm以下の値を記録する。そして、それは陰圧 (negative pressure)である。分子がよりゆるく引き寄せられるほど、圧力はマイナスとなる。
これらの陽圧と陰圧は、いかなる絶対的意味でもプラスやマイナスではない。それらは、基準圧力Patmに対してプラス(より上の)またはマイナス(より下の)であるだけである。図6-2は、図6-1で図式化される空気分子の連続的な集合と分散の結果を表す。図6-2で、A、B、Dと記された3本の横列は、図6-1(図6-1からの横列CとEは図6-2から省略されている)の同じ列と一致する。そして、空気分子運動の漸進的に変化している履歴において3つの異なる時間を示している。時間Aで、複数の点はスペース全体に配布され均一に示される。媒質が外部の力に影響を受けていないならばそのことは予想されるだろう 。分布全体に及ぶあらゆる点の圧力はPatmである。
時間Bで、この分布状態は、空間を通して低い密度と高い密度の領域が交互になるものに変わる。濃い陰影のついた領域は、高密度(図6-1の、時間B、位置2の場合のように 2つの分子が直接に接している時)を表す、そして、薄い陰影のついた領域は低密度(図6-1、時間D、位置2のように)を表す。時間Dでは、空間を通して密度が再び交互になるが、 それらの場所は、時間Bでのそれらと逆になっている。言い換えると、空間(例えば位置2)の特定の点にとって、時間Bで高密度で高圧域であるものは、時間Dでは低密度で低圧域である。高密度と高圧の領域は圧縮(compression)または圧縮度(condensation)(3)の領域と呼ばれている;低密度と低圧の領域は希薄(rarefaction)の領域と呼ばれている。
(注3)圧縮度(Condensation)は、圧縮(compression)の結果である。このテキストの目的上、圧縮と圧縮度は同じ意味で使われる。
個々の分子ではなく、圧力波は空間のなかを伝わり、空間と時間両方の機能として変化する
個々の空気分子の運動について以前に言われたことを思い出しなさい。それらは静止位置の前後に動き、その運動は内在する弾性と慣性力に起因する。しかし、分子自体はスペースを横切って広がっているのではない。スペースを横切るのは圧力波である。そして、図6-2に圧縮(圧縮度)と希薄の領域の連鎖として左から右に示される。これらの高低の圧力の交互の領域が、空気分子の前後の動き(それは、交互にそれらを集め分離する)になるので、スペースの特定の点では、時には高圧(図6-1の時間B、位置2のような)となり、時には低圧(図6-1と6-2の時間D、位置2のような)となる。このように、圧力波はある特定の瞬間(時間BまたはD全域で図6-2を検討する)にスペースを横切り、空間のある特定の場所(図6-2で、空間のあらゆる点で時間BとDを比較する)で変化する。
音波の源 (source)(空気分子の変位を起こす力のもと)から圧力波が移動するとき、上下の圧力の交互の部分は、図6-2の左から右に示されるように多くの場合直線で進む。これらの種類の音波は、高低の圧力の連鎖が、源から離れて広がる一連の圧力「スライス」(pressure “slices”)または平面とみなすことができるので、平面波(plane waves)と呼ばれる。当面の議論のために、平面波だけが考慮される、しかし、他の種類の圧力波は可能である(たとえば、源から直線で離れるよりはむしろ源から横に移動するもの) 。
時間と空間における圧力波のバリエーションは、測定することができる
圧力波の時間的(時間)空間的(スペース)バリエーションの特殊な測定法がある。これらの測定法の堅実な把握は、スピーチ生成についての音響理論の重要な測面を理解するための基本となり、第7章で取り上げられる。
時間的な測定(Temporal Measures)
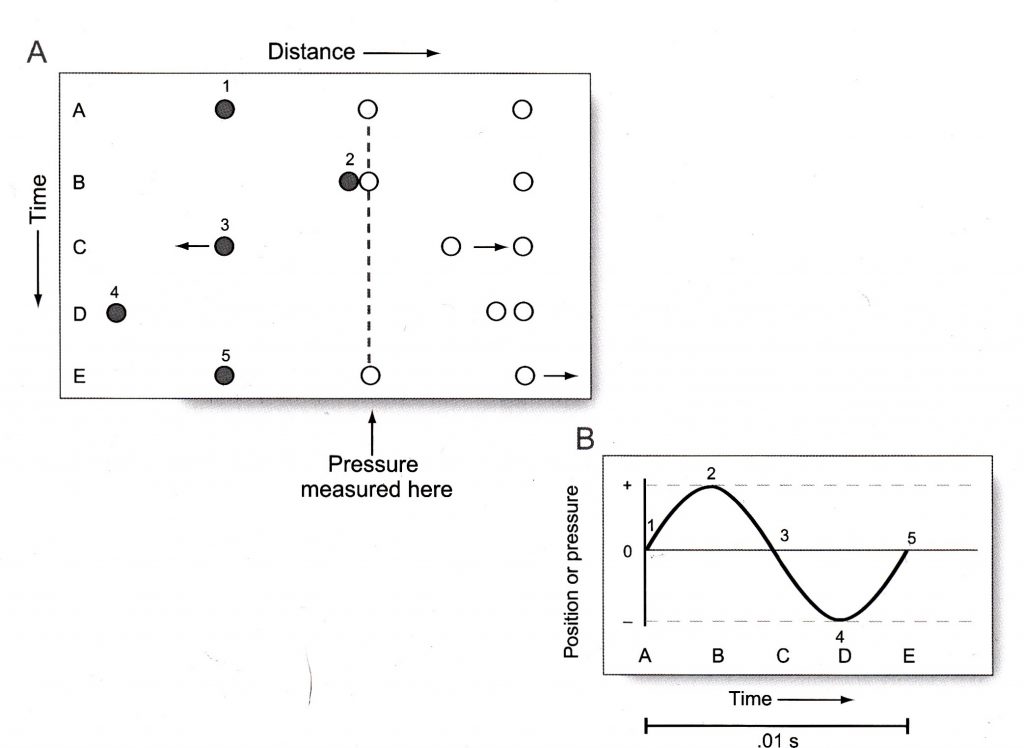
図 6-3.
A. 静止位置辺りの空気分子(満たされた円)の振動の概要モデル。
分子の上の数字は、その振動サイクル中の5つの連続する時点を示す。
B. 塗られたサークルの位置の図表と、1振動サイクル中の第2分子の位置で測られる圧力。
図6-3 Aは、図6-1で示された分子運動の一部を再描画している。特に興味深いのは、第1分子(図6-3 Aで濃い円として示される)の運動である。図6-1のように、スペース(間隔)は左から右に、そして、時間は上から下(連続して起こる時間A、B、C、D、E )で示される。濃い円上の番号1、2、3、4、5は、5つの別々の時点での第1分子の位置を示す。そして、分子が静止位置「1」から始まり、静止位置「5」に戻って終わる。時間Bで、分子は次の分子に接触し、上向きの矢で示されるスペースの場所で圧縮または高圧の領域をつくる。スペースのこの場所での圧力は、時間C(「3」の分子)でいくぶんマイナスになり、やがて時間D(「4」の分子)ではさらにマイナスになって、時間E(「5」の分子)で大気圧(Patm)に戻る。
濃い円の分子の運動は、図6- 3 Bの時間の関数として示される。あらゆる大きさ(例えば変位、圧力、速度、その他)が時間の関数として示されるとき、図表は波形 (waveform)と呼ばれる。この波形は、静止位置(1)から右端の(2)へ、静止位置(3)を通って戻り 左端の(4)へ、そして、最後に静止位置(5)に戻る分子の位置を示す。言い換えると、この波形は、分子の1つの完全な運動サイクル周期 (cycle of motion)を示す。分子がポイント5の後、動き続けるならば、それは5つの連鎖による1つを繰り返し、同じ運動履歴でもう一つのサイクルを生じるだろう。
図6- 3Bの波形のy軸は圧力としても分類される、なぜなら、空気圧(位置2で測量された)と第1分子の位置が時間経過とともに同じ様に変わることを示すのが簡単であるからだ。分子運動(図6-3Aの「2」)の最も右端は、圧力測定点で、空気圧縮が最大になる時でもあり、同時に最も左端(「4」)は、圧力測定点で希薄が最大となる、そして、静止位置(「1」と「5」)はPatmとなるだろう。これらの別々の時間の間の位置は、圧縮とPatmまたは希薄とPatmの間のどこかの圧力を持つ。このように、図6- 3Bの波形も、圧力波の時間的変化を示す。
周期(T)は、運動の1つの完全なサイクルを完成するためにかかる時間であり、次の式によって得られる:T = 1/f、f =周波数。
黒い円の分子は、図6- 3 Bで示す時間の連続関数 (a continuous of time)として曲線で示される。図6- 3 Aは5つの別々の時点を示すだけである、しかし、図6- 3 Bは時間AからEまでの分子のありうる全ての位置と、それらの位置が時間とともにどのように変わるかを示す。時間はx軸で、分子位置(または空気圧)はy軸で示される。波形の上下の半分を切り離している水平線は分子の静止位置を示す、つまり、そのとき 圧力= 大気圧 (Patm)である。図6-3 Aで与えられた番号1、2、3、4と5は、時間図表上の該当する場所を指し示す。図6- 3 Bで示されるような、時間の経過で繰り返される圧力波の時間的変動の測定は、1つの完全なサイクルを完成するために掛かる時間を計算することによってなされる。これは振動周期 (period)と呼ばれ、記号Tによって表示される。たとえば、図6-3 Bの波形で示される時間尺度によれば、1サイクルの分子運動を完了するには、.01秒が必要である。
したがって、この波形の場合
T = .01秒(s) あるいは、
T = 10ミリ秒(ms).
この例では、.01秒と10ミリ秒は同じ数値であるが異なる単位で表記される。スピーチと聴覚アプリケーションでは、msで時間単位を表すのが一般的である。参考のために、1 s = 1000 ms、0.1 s = 100 ms、0.01 s = 10 msと0.001 s = 1 ms。
図6- 3 Bで示されるような、反復する周期的運動の時間変動を表す別の方法は、周波数 (frequency)と呼ばれ、f の記号で表される。
周波数(f)は単に周期(T)の逆数で、式で示すと
f = 1/T 式(1)
周波数のための単位はHertzで、Hzと略される。そして、それは「秒当たりのサイクル」を表す。
式から生まれる数は、完全な振動サイクルが1 sの周期でどれくらい起こるかを示す。
たとえば ― 式(1)が図6- 3 Bで10 msの周期に当てはめられるならば、結果は
f = 1/10 msまたは
f = 1/0.01 = 100 Hz.
式によると、周波数(f)は周期(T)の逆数であり、1つの変数(例えば、f)が増加するとき、他(例えば、T)が減少することを意味する。このように、より長い周期は低い周波数と関連付けられ、そして、より短い周期はより高い周波数と関連付けする。
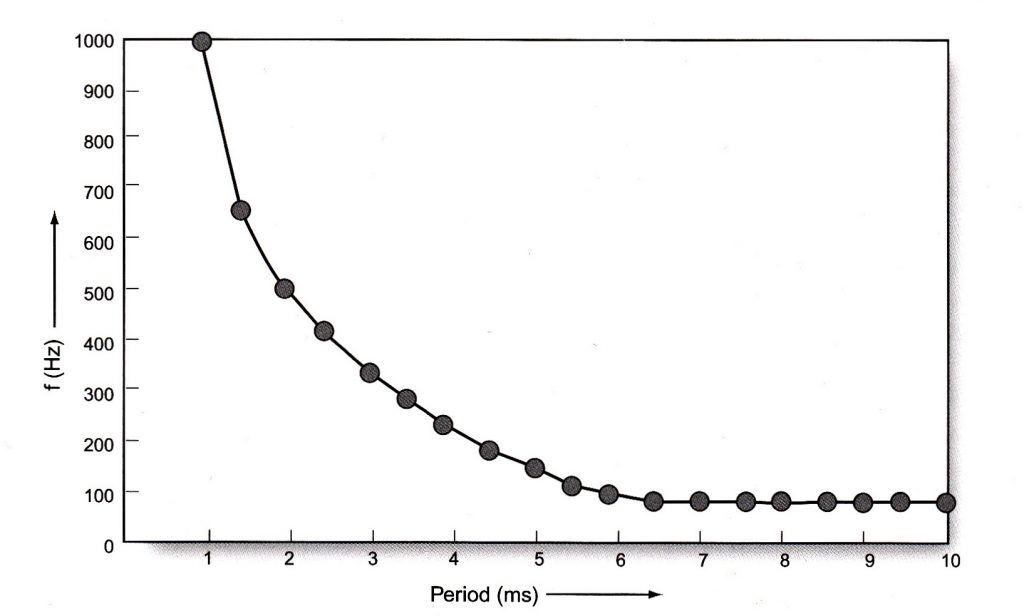
図6-4.
2つの変数の間の逆数と非線形の関係を示す周波数対周期の図表。
図6-4は、10.0 msの間で1.0 msに変動する周波数と周期の関係を表す。このグラフで、周期はx軸で記されて、0.5 ms(すなわち、10.0 ms、9.5 ms、9.0 ms、8.5 ms、…1.0 ms)の幅で変わる。対応する周波数値(f = 1/Tで計算される)は、y軸で記される。逆の関係、そこでは長い周期が低い周波数と関係する、はx軸上の値が増加(x軸で密接した変化)するにつれて、y軸上での曲線で示された点が下がるという進行が明らかに見られる。また、Tとfの関係は線形 (linear)でない点に注意しなさい。2つの変数の完全に線形の関係においては、ある変数の等しい大きさの変化が、他の変数の等しい大きさの変化を伴う。Tとfの関係が完全に線形であるならば、Tの各々の0.5‐msの間隔はfの一定の変化を伴うだろう。しかし、図6-4の中で、10 ms(x軸)辺りでの0.5‐msのステップを伴う周波数変化(y軸)は、1.0 ms辺りの0.5‐msのステップを伴う周波数変化より明らかに非常に小さい。たとえば、x軸の上の9.0と9.5 msの間の0.5‐msの変化はおよそ6 Hzのfの変化をもたらす、しかし、2.5と3.0 msの間の同じ0.5‐msの変化は65 Hz以上のfの変化をもたらす。図6-4の中の個々の点が実線によってつながれるとき、2つの変数の関係は明らかにカーブする。この種の関係(1つの変数に沿った等しい間隔は第2の変数の上で等しい間隔を生じない)は、非線形 (nonlinear) や曲線 (curvilinear) の関係と呼ばれている。
空間的測定 (Spatial Measures)
図6-5.
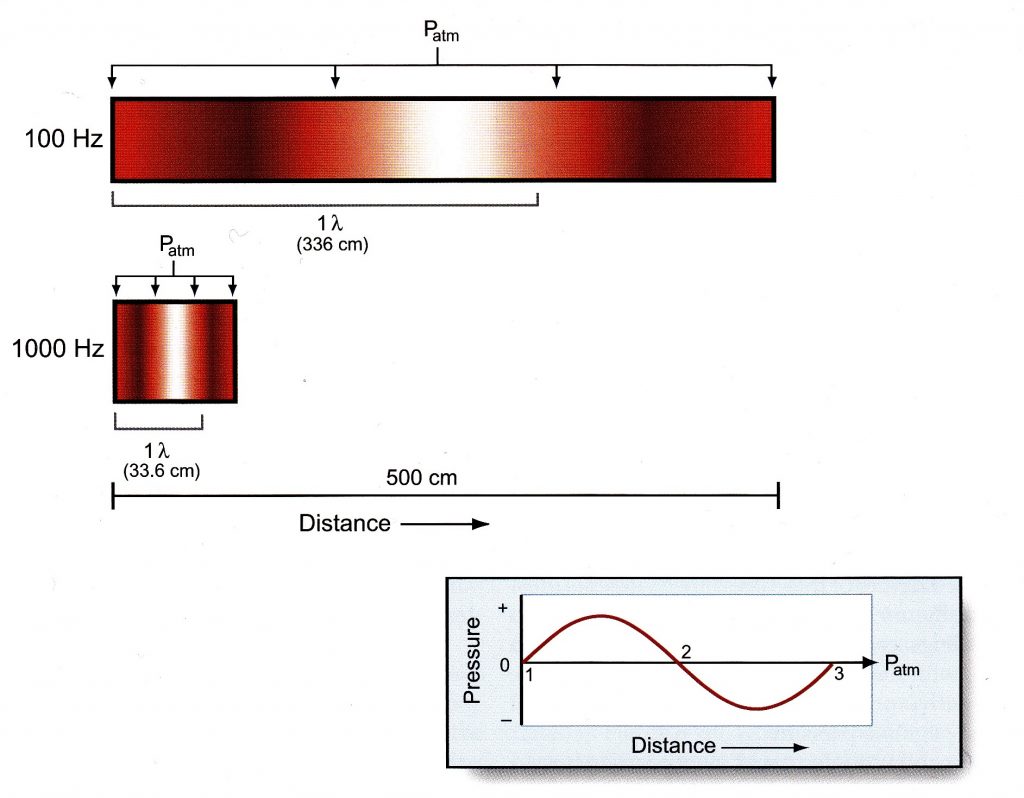
波長の測定の図解。
波長は、圧力変動のサイクルに適用される距離である。
この距離は、100‐Hzと1000‐Hzの信号での1λと記される。
図6-2で、圧力波は「スペースを横切って高/低の圧力の領域を交替させる」と説明された。2つの圧力波の部分が図6-5に示される。1つは100 Hzの周波数と一致する、そして、もう1つは1000 Hzの周波数と一致する。x軸は、距離として、0から500 cm(およそ0~195インチに等しい)まで測定される。図6-5に示される両周波数の圧力波の一部は、高・低の圧力の領域の連鎖から成る。濃く陰影のついた領域(空気分子の比較的高密度の集合を示す)の高圧領域と薄く陰影のついた領域(分子を比較的まばらに詰め込むことを示す)の低圧領域が示されている。100 Hzの音に関連する高・低の圧力間のスペースを通しての1つの完全な変化は、1000 Hzの音のスペースを通してそれに相当する変化より大きな距離になることがすぐにわかる。 圧力波のスペース変化の外形の寸法は波長 (wave length)と呼ばれている。そして、それは単に高圧領域とその次の低圧の領域(または、低圧の領域とその次の高圧領域)にわたる距離である。波長はギリシア文字ラムダ(λ)によって象徴されて、図6-5に示された両方の圧力波が、第1高圧領域の最先端から次の高圧領域の最先端に伸びているのを示す。すぐ上で与えられた定義と一致して、これは、最初の高圧領域とその次の低圧領域をカバーする間隔を含む。
波長は、周波数と反比例の関係にある。周波数が高いほど、波長は短い。この音響法則は図 6-5で例示される、そこでは1000 Hzの音が100 Hzの音よりかなり短い波長を持つ 。波長の式は、以下の通りである:
λ= c/f または f=c/λ 式 (2)
そこでは、空気中の音の f =周波数、そして、c =速度、そしてそれは定数で、およそ33,600 cm/s(およそ1100フィート/s)の値を持つ。図6-5に示される周波数の値が定数cの値とともに式にはめるならば、100 Hzと1000 Hzのための波長はおよそ336 cm(100 Hz)と33.6 cm(1000 Hz)であるとわかる。したがって、空間的変動 (spatial variation)は単純な距離によって判断される。
また、図6-5の中の低圧と高圧領域の「境界」が大気圧 (Patm)であることを示されている点に注意しなさい。先に述べたように、これは、圧力がスペースを通して変化するとき、圧力がPatmと等しい点があることを示す。圧力は、Patmより、その上下その他に行くことによってスペースを通して変化する。スペースを通しての圧力の変化は、段階的である。高・低の圧力領域について話すとき、それらの領域は最大の陽圧または陰圧を有すると云われる。これらの圧力の段階的な性質は、最もプラスで起こる濃い陰影と最もマイナスで起こる薄い陰影による、圧縮と希薄の領域の微妙な違いで変化する。
一つの波長の圧力の連続変化は図6-5への差し込み図にも示されている、そこで、圧力(y軸)は距離(x軸)の関数として示される。この差し込み図の水平線は、Patm(基準圧力)である。圧力は、陽圧のピークに達するまで、Patm(差し込み図の「1」)に対する増加が見られ、それから減少してPatm(差し込み図の「3」)を通過する。これは、図形の主要部で示される圧力波を曲線で示す異なる方法である。声道(声帯と唇の調音器官で形づくられる空気の「チューブ」)の調音形状と音響出力を扱っている第7章のセクションで明らかになるように、波長の概念は、異なる調音が異なる母音になるわけを理解するためにきわめて重要である。
圧力波:まとめと正弦曲線の導入
空気分子の活動は圧力波を生み出すことができる。そして、それは音の基盤である。圧力波は空間と時間にわたって変化する、そして、両方の変化は単純な数学を使用して記述され測定されることができる。
この時点まで、これらの現象の例と説明は、図式的だったか、ある程度まで単純化されてきた。たとえば、これらの空気分子の動作と、結果として生じる圧力波の原因または源についてごくわずかしか説明されなかった。そして、議論される特定の動作は非常に単純である、ところが、スピーチのような多くの音響現象は空気分子の非常に複雑な振動、そして、それらの振動の非常に複雑な音源を必要とする。しかし、最も複雑な振動さえ上述の単純な振動のセットまたはグループに分析されることは事実である。また、これらの単純な動作の一組を取り出しそれらを互いに合わせることによって複雑な振動が作り出されることができることも事実である。言い換えると、複雑な音響現象は、多くの個々の単純な音響現象を結合することによってつくられることができる。このように、単純な振動の理解は、ほとんどの音響現象で見られる、更に複雑な振動を理解するための基礎である。
上述の単純な動作と結果として生じる圧力波は、正弦曲線運動そして正弦波と呼ばれている。正弦曲線運動は振動で最も単純な形である。より複雑な振動は、一組の個々の正弦曲線に分析されることができる。複雑な音響現象は、一群の正弦曲線が一緒に結合されたときに起こる。正弦曲線運動の改まった説明は、複合音が単にそれらの成分をなす正弦曲線の総計であるという考えとともに次に提示される。
<サウンド・スピード>
大気中の音速は、気温の作用で異なり、湿気と高度の作用としてはより小さい程度に異なる。温度が高いほど、音波の伝播は速くなる。学生は、異なるテキストでわずかに異なる数値が使われるのがわかるだろう。33,600 cm/sは、摂氏0度(華氏32度)で測定されたおおまかな数値である。音速も、伝導媒質の性質によって異なる。音の伝搬は、空気と比較して水の中でおよそ4倍、鋼でおよそ11倍速い(誰でも、かなり遠くの距離から近づいてくる電車を「聞く」ために耳を鉄道の線路に置くこつを知っている)。一般的なルールは:媒質がより濃いほど、音響伝導はより速い。
2019/05/13 訳:山本隆則